SPARK 18 Release Notes¶

We present here a few highlights of the new features in SPARK 18. You can access the complete list here.

Program Specification ¶

Preconditions on Standard Numerical Functions ¶

Preconditions have been added to functions from the standard numerical package Ada.Numerics.Generic_Elementary_Functions, in cases that may lead to Numerics.Argument_Error or Constraint_Error when called on actual parameters that are not suitable, like a negative input for Sqrt. This ensures that GNATprove generates corresponding precondition checks when such functions are called. For example, here are the preconditions on Sqrt and Log:

function Sqrt (X : Float_Type'Base) return Float_Type'Base with
  Pre  => X >= 0.0,
  ...

function Log (X : Float_Type'Base) return Float_Type'Base with
  Pre  => X > 0.0,
  ...

Contracts on Formal Containers ¶

The formal containers library, which provides SPARK-compatible versions of Ada containers, has been enriched with comprehensive contracts. These contracts use functional, mathematical-like containers as models of imperative containers. For example, here is the contract of function Element which expresses that the value returned is the value found in the functional model of the list (which is a sequence) at the index corresponding to the cursor Position obtained from the functional model of cursor positions (which is a map):

function Element
  (Container : List;
   Position : Cursor) return Element_Type
with
  Global => null,
  Pre    => Has_Element (Container, Position),
  Post   =>
    Element'Result =
      Element (Model (Container), P.Get (Positions (Container), Position));

These precise contracts can now be used to express more easily rich functional properties on programs that manipulate formal containers. For more details, see the description of the formal containers library in the SPARK User’s Guide. The loop examples in the SPARK User’s Guide have been updated to use these new specification capabilities.

Specification of Subprogram Termination ¶

It is now possible to specify that a subprogram is always terminating, for every value of its inputs allowed in its precondition. This in turns allows for easier proof of its callers in some cases. This is specified as follows:

function F (X : Natural) return Natural;
pragma Annotate (GNATprove, Terminating, F);

GNATprove checks that property during flow analysis and emits a message if it cannot guarantee termination. See the SPARK User’s Guide for more details.

Proof Automation ¶

Better Integration of CodePeer ¶

The engine of static analyzer CodePeer was integrated in SPARK Pro 17 to prove run-time checks and assertions in addition to the other distributed provers Alt-Ergo, CVC4 and Z3. The initial integration did not allow to benefit from the full capability of CodePeer. In particular, assertions (including pragma Assert and loop invariants) and checks on possible division by zero that were proved by CodePeer needed to be reproved by other provers in GNATprove. Additionally, the integration was not working in various scenarios, depending on the specific options selected or the particular project file configuration.

All these problems in the integration of CodePeer have been fixed, which allows to fully benefit from the use of static analysis in GNATprove. CodePeer is activated by using the switch --codepeer=on on the command line, or by selecting the checkbox CodePeer Static Analysis in the proof dialog opened in GPS after selecting the SPARK ‣ Prove All, SPARK ‣ Prove File and similar menu entries.

Unrolling of Simple For-Loops ¶

In general, proving properties of code with loops requires writing loop invariants. This is not necessary anymore when the loop is simple enough, which entails in particular that it contains fewer than 20 iterations, and it does not come with a loop invariant already. See the SPARK User’s Guide for a precise definition of simple loops.

GNATprove now unrolls automatically simple loops. So a loop over 10 elements in an array A such as:

for J in Index loop
   A (J) := J;
end loop;

is analyzed by GNATprove as if it was written without loop:

A (1) := 1;
A (2) := 2;
A (3) := 3;
A (4) := 4;
A (5) := 5;
A (6) := 6;
A (7) := 7;
A (8) := 8;
A (9) := 9;
A (10) := 10;

In cases where a user does not want a loop to be unrolled this way, she can either:

add a dummy loop invariant pragma Loop_Invariant (True); in the loop; or
call GNATprove with the switch --no-loop-unrolling.

See also the blog post on Proving Loops Without Loop Invariants.

Enhanced Library of Lemmas for Floating-Point Arithmetic ¶

Some checks involving floating-point computations are particularly difficult to prove automatically, in particular when they don’t depend simply on computing coarse static bounds for the result of computations. This is related to the weaker support for floating-point arithmetic in provers, compared to the support of integer arithmetic.

We introduced a library of lemmas in SPARK Pro 17, that can be used to prove more complex properties that cannot be proved fully automatically, with manageable complexity for the user. We have now added lemmas about the monotonicity of floating-point operators. Thus, to prove that X * Z is less than Y * Z when X is known to be less than Y and Z is non-negative, all of them being floating-point variables, one can simply call the corresponding ghost procedure from the SPARK lemma library:

SPARK.Float_Arithmetic_Lemmas.Lemma_Mul_Is_Monotonic (X, Y, Z);
--  here X * Z <= Y * Z is known

GNATprove will verify the conditions for using the lemma as specified in its precondition. In the case above, these include X <= Y and Z >= 0.0.

See the SPARK User’s Guide for more details.

Better Tracking of Dynamic Types ¶

GNATprove more precisely tracks the dynamic type of tagged types (types used for Object Oriented programming in SPARK), both for variables and function results whose actual type is known statically. This translates in more precise proof of dispatching calls on such variables, as GNATprove can use the more precise contract when the controlling type of the dispatching call is known.

Proof Interaction ¶

Manual Proof in GPS ¶

The use of manual proof allows to address more complex properties than cannot be proved fully automatically, with manageable complexity for the user, represented by the manual proof label in the following diagram:

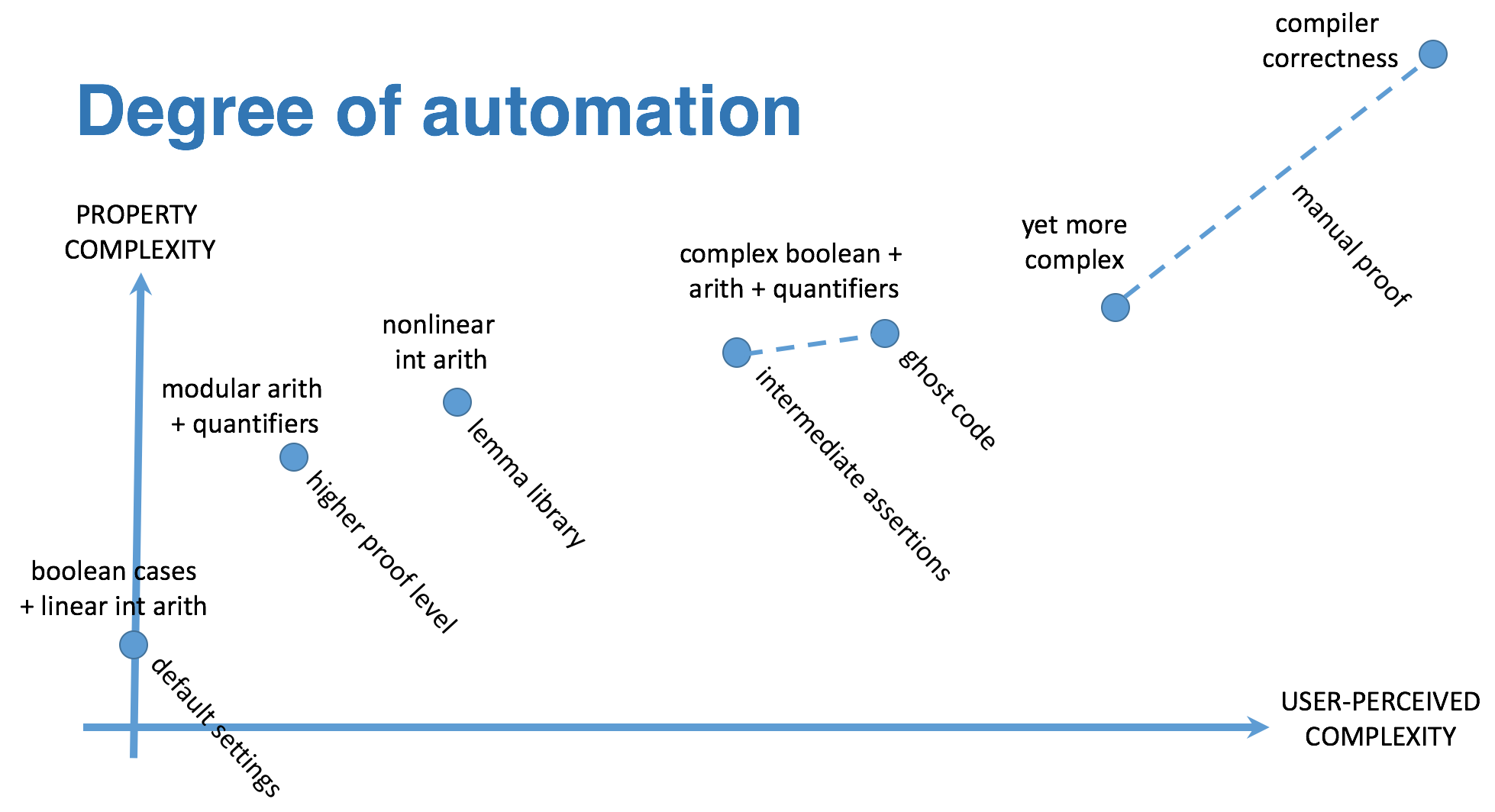
With manual proof, the user can interactively manipulate the proof context for proving a property. With transformations (so-called tactics in the scientific literature on interactive proof), the user can modify the proof context to make it easier to solve by provers or to complete the proof manually. The following interface for manual proof is started by selecting the contextual menu SPARK ‣ Start Manual Proof on an unproved check message inside GPS:

As much as possible, the names of logic elements in the proof context follow the naming of variables from the program. When the proof is complete, the actions of the user are saved in the proof session file, which can be stored and shared under version control.

Better Support for Interactive Provers ¶

Private types whose full view is not in SPARK are now translated into clones of the predefined __private Why3 abstract type, with unique names in Why3. This allows to more easily map them to distinct existing logic types in interactive provers.

Machine-Parsable Information on Proof Attempts ¶

The precise list of Verification Conditions that were generated by GNATprove, and which provers were called on each one, is now output by GNATprove in a machine-parsable format in the .spark files that are produced for every analyzed unit. The content of these files is documented in the SPARK User’s Guide.

For an example of use of this data, see this blog post on third-party tools that compute statistics on GNATprove analysis results.

Tool Usability ¶

Support for CWE Ids ¶

Users can get CWE ids in messages by using the new switch --cwe. For example, on a possible division by zero, GNATprove will issue a message including CWE 369:

file.adb:12:37: medium: divide by zero might fail [CWE 369]

This allows for easier analysis of messages based on the underlying vulnerabilities, for use in a security context.

For more information on CWE, see the MITRE Corporation’s Common Weakness Enumeration (CWE) Compatibility and Effectiveness Program (http://cwe.mitre.org/).

Easier Tool Configuration ¶

Until SPARK Pro 17, extra setup was required to make GNATprove work with a non-default runtime, even when the project file contained all the information. Now, GNATprove uses the same mechanism to find the runtimes for formal verification as GPRbuild does for compilation: as long as all required tools are installed and on the PATH, SPARK will find and use the correct runtime according to the --RTS and --target switches passed to it, or the Runtime and Target attributes defined in the project.

Support for Caching Using memcached ¶

The SPARK tools now support caching large parts of the analysis via a memcached server. If a memcached server is available to store analysis results, and this server is specified to GNATprove via the command line option --memcached-server=hostname:portnumber, then subsequent invocations of the tools, even across different machines, can store intermediate results of the tools. The user-visible effect is that GNATprove can produce results faster.

See this blog post for more details.