Getting Started

SPARK 2014 is a programming language and a set of verification tools designed to meet the needs of high-assurance software development. SPARK 2014 is based on Ada 2012, both subsetting the language to remove features that defy verification, but also extending the system of contracts and “aspects” to support modular, formal verification.

SPARK 2014 is a much larger and more flexible language than its predecessor SPARK 2005. The language can be configured to suit a number of application domains and standards, from server-class high-assurance systems (such as air-traffic management applications), to embedded, hard real-time, critical systems (such as avionic systems complying with DO-178C Level A).

SPARK 2014 is supported by various tools in the GNAT Pro toolsuite:

• the GNAT compiler
• the GNATtest tool for unit testing harness generation
• the GNATprove tool for formal program verification

A user can specify in SPARK 2014 the functional behavior of a program, and get the following results from the above tools:

• errors and warnings during compilation;
• exceptions being raised at run time when an assertion fails, if the program is compiled with appropriate switches;
• a unit testing harness taking into account subprogram contracts, generated by GNATtest;
• formal guarantees that a set of subprograms are free from run-time errors and respect their contracts, provided by GNATprove.

A crucial feature of GNATprove is that it interprets annotations exactly like they are interpreted at run time during tests. In particular, their executable semantics includes the verification of run-time checks, which can be verified statically with GNATprove. GNATprove also performs additional verifications on the specification of the expected behavior itself, and its correspondence to the code.

This chapter describes a simple use of the SPARK 2014 toolset on a program written completely in SPARK 2014. Other chapters give a more complete overview of the different parts of the SPARK 2014 technology:

• Chapter Introduction to SPARK 2014 provides a detailed introduction to the SPARK 2014 language.
• Chapter Formal Verification with GNATprove describes the use of the GNATprove formal verification tool.
• Chapter Usage Scenarios for Formal Verification lists the main usage scenarios for formal verification.
• Chapter Combining Formal Verification and Testing explains how to combine the results of formal verification and classical verification by testing.

In this chapter, we use the integration of the SPARK 2014 toolset in the GPS integrated development environment. The same functionalities are available in command-line as well, see Command-line Options.

Writing SPARK 2014 Programs

A SPARK 2014 program is a valid Ada program, which can be compiled by the GNAT Pro compiler, edited in the GPS or GNATbench editors, and debugged/analyzed/modified with the associated GNAT Pro toolset.

All kinds of data types defined in Ada can be defined in SPARK 2014, except access types. The main restriction on expressions in SPARK 2014 is that they should not contain calls to functions which modify the value of non-local variables. Most statements in Ada are allowed in SPARK 2014, at the notable exception of goto statements and raise statements. These restrictions correspond to existing coding standard rules for critical software, and do not prevent the natural expression of data-structures and algorithms used in critical software.

As a running example, we consider the naive searching algorithm in an unordered collection of elements. The algorithm returns whether the collection contains the desired value, and if so, at which index. The collection is implemented here as an array. We start on purpose with an incorrect program for package Search, in order to explain how the SPARK 2014 toolset can help correcting these errors.

We start with creating a GNAT project file in search.gpr:

project Search is
   for Source_Dirs use (".");

   package Compiler is
      for Default_Switches ("Ada") use ("-gnatwa");
   end Compiler;
end Search;

It specifies that the source code to inspect is in the current directory, and that the code should be compiled at maximum warning level (switch -gnatwa). GNAT projects are used by most tools in the GNAT Pro toolsuite; for an in-depth documentation of this technology, you may consult GNAT Pro User’s Guide.

The obvious specification of Search is given in file search.ads:

package Search is

   type Index is range 1 .. 10;
   type Element is new Integer;

   type Arr is array (Index) of Element;

   function Linear_Search
     (A        : Arr;
      Val      : Element;
      At_Index : out Index) return Boolean;
   --  Returns True if A contains value Val, in which case it also returns
   --  in At_Index the first index with value Val. Returns False otherwise.

end Search;

The implementation of Search given in file search.adb is as obvious as its specification, using a loop to go through the array A given in parameter and looking for the first index at which Val is found, if there is such an index:

package body Search is

   function Linear_Search
     (A        : Arr;
      Val      : Element;
      At_Index : out Index) return Boolean
   is
      Pos : Index := A'First;
   begin
      while Pos < A'Last loop
         if A(Pos) = Val then
            At_Index := Pos;
            return True;
         end if;

         Pos := Pos + 1;
      end loop;

      return False;
   end Linear_Search;

end Search;

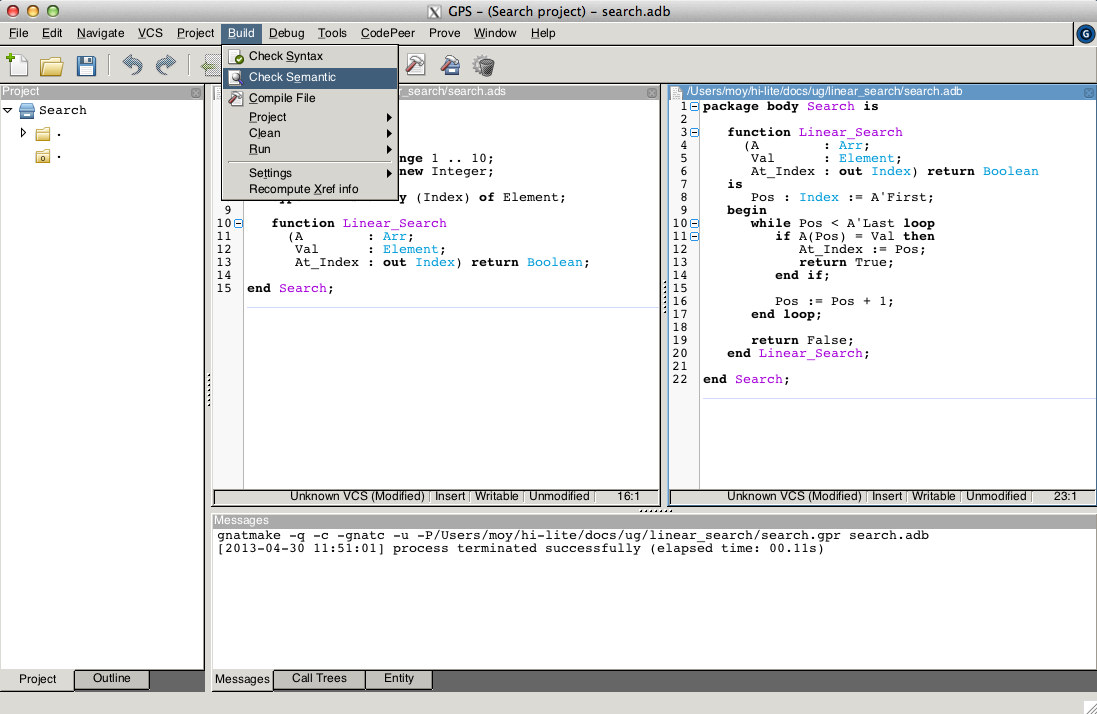
We can check that the above code is valid Ada code by using the Build::Check Semantic menu, which completes without any errors or warnings:

To state that this code should be valid SPARK 2014 code, we can add the SPARK_Mode pragma in the sources as a local pragma, or in a configuration file as a configuration pragma. We consider here the former case, where the following line is added on the first line of search.ads:

pragma SPARK_Mode (On);

Then, we run GNATprove in mode check, using the Prove::Prove File menu, so that it issues errors on code that has SPARK_Mode=On but is not in SPARK:

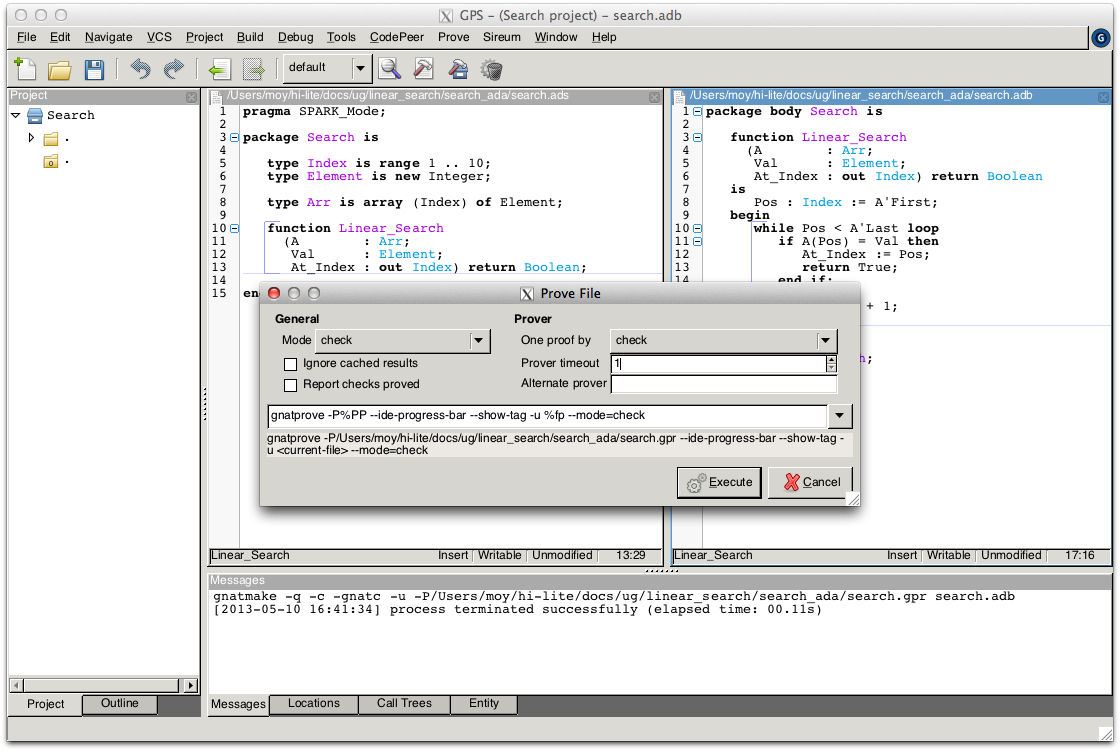
It detects here that function Linear_Search is not in SPARK, because it has an out parameter:

This recent permission in Ada to have out parameters in functions is not allowed in SPARK 2014, because it causes calls to have side-effects (assigning to their out parameters), which means that various calls in the same expression may be conflicting, yielding different results depending on the order of evaluation of the expression.

We correct this problem by defining a record type Search_Result holding both the boolean result and the index for cases when the value is found, and making Linear_Search return this type:

 pragma SPARK_Mode (On);

 package Search is

    type Index is range 1 .. 10;
    type Element is new Integer;

    type Arr is array (Index) of Element;

    type Search_Result is record
       Found    : Boolean;
       At_Index : Index;
    end record;

    function Linear_Search
      (A   : Arr;
       Val : Element) return Search_Result;

 end Search;

The implementation of Linear_Search is modified to use this type:

 pragma SPARK_Mode (On);

 package body Search is

    function Linear_Search
      (A   : Arr;
       Val : Element) return Search_Result
    is
       Pos : Index := A'First;
       Res : Search_Result;
    begin
       while Pos < A'Last loop
          if A(Pos) = Val then
             Res.At_Index := Pos;
             Res.Found := True;
             return Res;
          end if;

          Pos := Pos + 1;
       end loop;

       Res.Found := False;
       return Res;
    end Linear_Search;

 end Search;

GNATprove runs without errors in mode check on this program, which is thus valid SPARK 2014 code. It is not yet very interesting SPARK 2014 code though, as it does not contain any contracts, which are necessary to be able to apply formal verification modularly on each subprogram, independently of the implementation of other subprograms. The precondition constrains the value of input parameters, while the postcondition states desired properties of the result of the function. Here, we can require in the precondition that callers of Linear_Search always pass a non-negative value for parameter Val, and we can state that, when the search succeeds, the index returned points to the desired value in the array:

function Linear_Search
  (A   : Arr;
   Val : Element) return Search_Result
with
  Pre  => Val >= 0,
  Post => (if Linear_Search'Result.Found then
             A (Linear_Search'Result.At_Index) = Val);

Notice the use of an if-expression in the postcondition to express an implication: the search succeeds implies that the value at the returned index is the searched one. Note also the use of Linear_Search'Result to denote the value returned by the function.

This contract is still not very strong. Many faulty implementations of the search would pass this contract, for example one that always fails (thus returning with Linear_Search'Result.Found = False). We could reinforce the postcondition, but we choose here to do it through a contract by cases, which adds further constraints to the usual contract by precondition and postcondition. We want to consider here three cases:

• the desired value is found at the first index (1)
• the desired value is found at other indexes (2 to 10)
• the desired value is not found in the range 1 to 10

In the first case, we want to state that the index returned is 1. In the second case, we want to state that the search succeeds. In the third case, we want to state that the search fails. We use a helper function Value_Found_In_Range to express that a value Val is found in an array A within given bounds Low and Up:

function Value_Found_In_Range
  (A       : Arr;
   Val     : Element;
   Low, Up : Index) return Boolean
is (for some J in Low .. Up => A(J) = Val);

function Linear_Search
  (A   : Arr;
   Val : Element) return Search_Result
with
  Pre  => Val >= 0,
  Post => (if Linear_Search'Result.Found then
             A (Linear_Search'Result.At_Index) = Val),
  Contract_Cases =>
    (A(1) = Val =>
       Linear_Search'Result.At_Index = 1,
     Value_Found_In_Range (A, Val, 2, 10) =>
       Linear_Search'Result.Found,
     (for all J in Arr'Range => A(J) /= Val) =>
       not Linear_Search'Result.Found);

Note that we express Value_Found_In_Range as an expression function, a function whose body consists in a single expression, which can be given in a specification file.

Note also the use of quantified expressions to express properties over collections: for some in Value_Found_In_Range expresses an existential property (there exists an index in this range such that ...), for all in the third contract case expresses a universal property (all indexes in this range satisfy are such that ...).

Each contract case consists in a guard (on the left of the arrow symbol) evaluated on subprogram entry, and a consequence (on the right of the arrow symbol) evaluated on subprogram exit. The special expression Linear_Search'Result may be used in consequence expressions. The three guards here should cover all possible cases, and be disjoint. When a contract case is activated (meaning its guard holds on entry), its consequence should hold on exit.

The program obtained so far is a valid SPARK 2014 program, which GNAT Pro analyzes semantically without errors or warnings.

Compiling SPARK 2014 Programs

We can compile the above program, and test it on a set of selected inputs. The following testing program exercizes both the case where the searched value is present or not in the array:

with Search;      use Search;
with Ada.Text_IO; use Ada.Text_IO;

procedure Test_Search is
   A   : constant Arr := (1, 5, 3, 8, 8, 2, 0, 1, 0, 4);
   Res : Search_Result;

begin
   Res := Linear_Search (A, 1);
   if Res.Found then
      if Res.At_Index = 1 then
         Put_Line ("OK: Found existing value at first index");
      else
         Put_Line ("not OK: Found existing value at other index");
      end if;
   else
      Put_Line ("not OK: Did not find existing value");
   end if;

   Res := Linear_Search (A, 6);
   if not Res.Found then
      Put_Line ("OK: Did not find non-existing value");
   else
      Put_Line ("not OK: Found non-existing value");
   end if;
end Test_Search;

We can check that the implementation of Search passes this test by compiling and running the test program:

$ gnatmake test_search.adb
$ test_search
> OK: Found existing value at first index
> OK: Did not find non-existing value

But only part of the program was really tested, as the contract was not checked during execution. To check the contract at run time, we recompile with the switch -gnata (a for assertions, plus switch -f to force recompilation of sources that have not changed):

• a check is inserted that the precondition holds on subprogram entry
• a check is inserted that the postcondition holds on subprogram exit
• a check is inserted that the guards of contract cases are disjoint on subprogram entry (no two cases are activated at the same time)
• a check is inserted that the guards of contract cases are complete on subprogram entry (one case must be activated)
• a check is inserted that the consequence of the activated contract case holds on subprogram exit

Note that the evaluation of the above assertions may also trigger other run-time check failures, like an index out of bounds. With these additional run-time checks, an error is reported when running the test program:

$ gnatmake -gnata -f test_search.adb
$ test_search
> raised SYSTEM.ASSERTIONS.ASSERT_FAILURE : contract cases overlap for subprogram linear_search

It appears that two contract cases for Linear_Search are activated at the same time! More information can be generated at run time if the code is compiler with the switch -gnateE:

$ gnatmake -gnata -gnateE -f test_search.adb
$ test_search
> raised SYSTEM.ASSERTIONS.ASSERT_FAILURE : contract cases overlap for subprogram linear_search
>   case guard at search.ads:29 evaluates to True
>   case guard at search.ads:31 evaluates to True

It shows here that the guards of the first and second contract cases hold at the same time. This failure in annotations can be debugged with gdb like a failure in the code (provided the program was compiled with appropriate switches, like -g -O0). The stack trace inside GPS shows that the error occurs on the first call to Linear_Search in the test program:

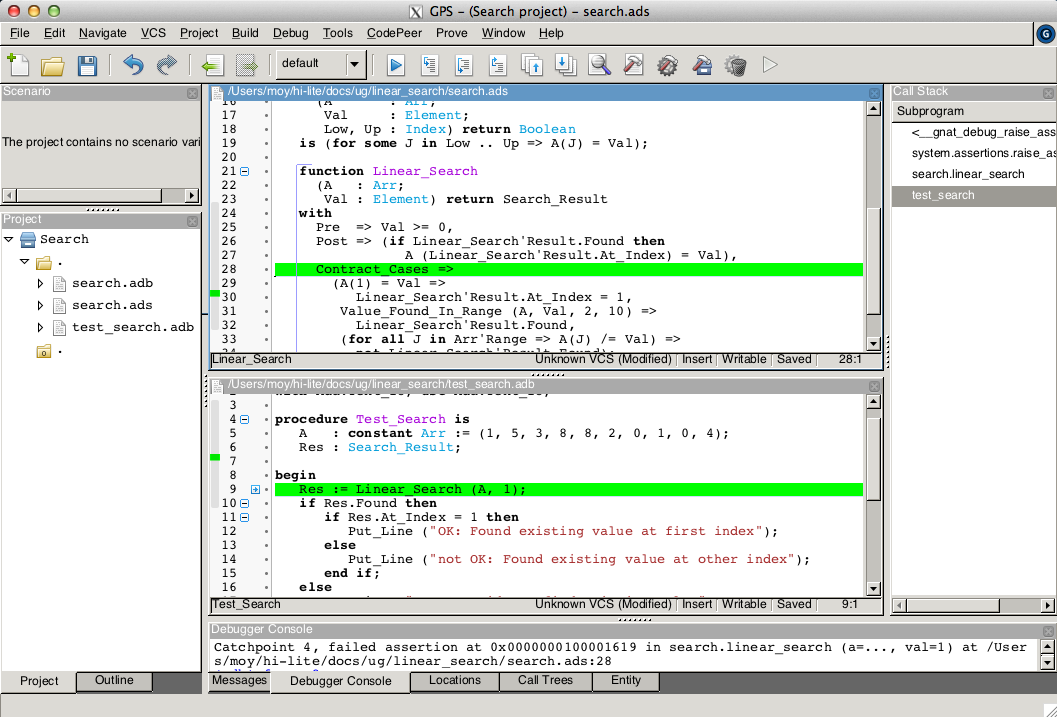
Indeed, the value 1 is present twice in the array, at indexes 1 and 8, which makes the two guards A(1) = Val and Value_Found_In_Range (A, Val, 2, 10 evaluate to True. We correct the contract of Linear_Search by strengthening the guard of the second contract case, so that it only applies when the value is not found at index 1:

Contract_Cases =>
  (A(1) = Val =>
     Linear_Search'Result.At_Index = 1,
   A(1) /= Val and then Value_Found_In_Range (A, Val, 2, 10) =>
     Linear_Search'Result.Found,
   (for all J in Arr'Range => A(J) /= Val) =>
     not Linear_Search'Result.Found);

With this updated contract, the test passes again, but this time with assertions checked at run time:

$ gnatmake -gnata test_search.adb
$ test_search
> OK: Found existing value at first index
> OK: Did not find non-existing value

The program obtained so far passes successfully a test campaign (of one test!) that achieves 100% coverage for all the common coverage criteria, once impossible paths have been ruled out: statement coverage, condition coverage, the MC/DC coverage used in avionics, and even the full static path coverage.

Verifying Formally SPARK 2014 Programs

Formal verification of SPARK 2014 programs is a two-step process:

1. the first step checks that flows through the program correctly implement the specified flows (if any), and that all values read are initialized.
2. the second step checks that the program correctly implement its specified contracts (if any), and that no run-time error can be raised.

Step 1 is implemented as a static analysis pass in the tool GNATprove, under the flow mode. This mode is still experimental, so many SPARK 2014 features are not yet supported. Step 2 is implemented as a deductive verification pass in the tool GNATprove, under the default prove mode. This mode is well developed, but a few SPARK 2014 features are still not yet supported.

The difference between these two steps should be emphasized. Static analysis in step 1 is a terminating algorithm, which typically takes 2 to 10 times the compilation time to complete. Deductive verification in step 2 is based on the generation of logical formulas for each check to prove, which are then passed on to an automatic prover to decide whether the logical formula holds or not. The generation of logical formulas is a translation phase, which typically takes 10 times the compilation time to complete. The automatic proof of logical formulas may take very long, or never terminate, hence the use of a timeout (default=1s) for each call to the automatic prover. It is this last step which takes the most time when calling GNATprove on a program, but it is also a step which can be completely parallelized (using switch -j to specify the number of parallel processes): each logical formula can be proved independently, so the more the number of available cores, the faster it completes.

Note

The proof results presented in this tutorial may slightly vary from the results you obtain on your machine, as the automatic prover may take more or less time to complete a proof depending on the platform and machine used.

We start with the flow analysis of Search, using the yet experimental mode flow of GNATprove reached through the Prove::Prove File menu:

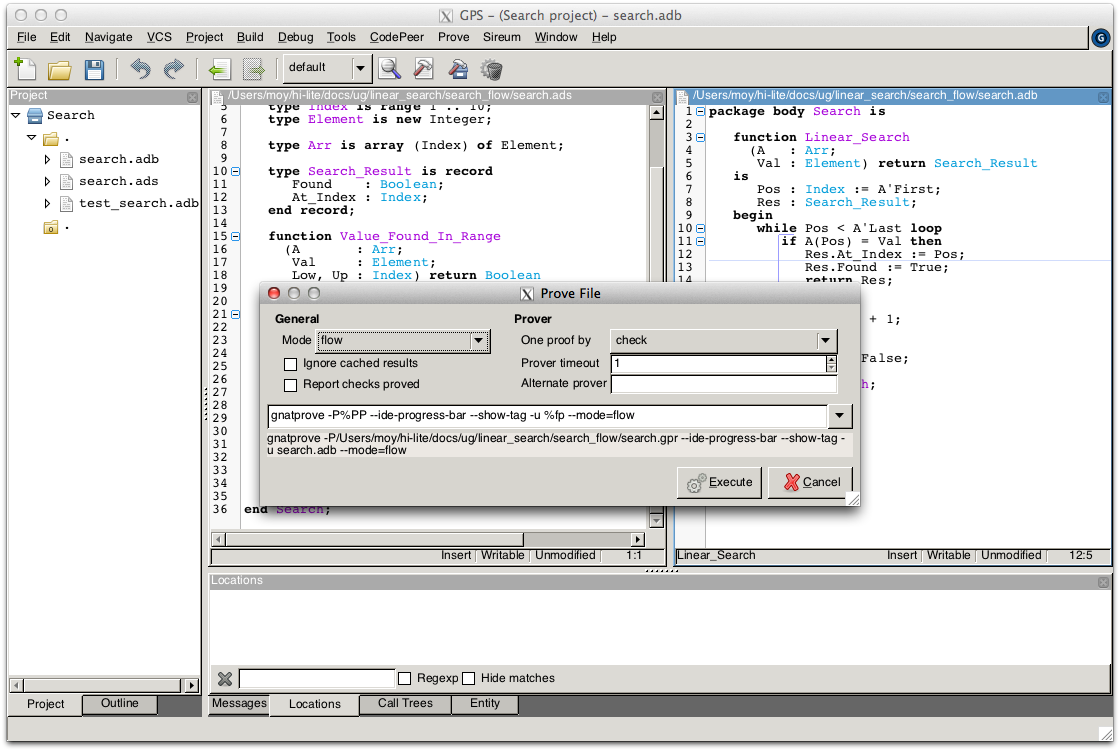
Here, it issues an error message:

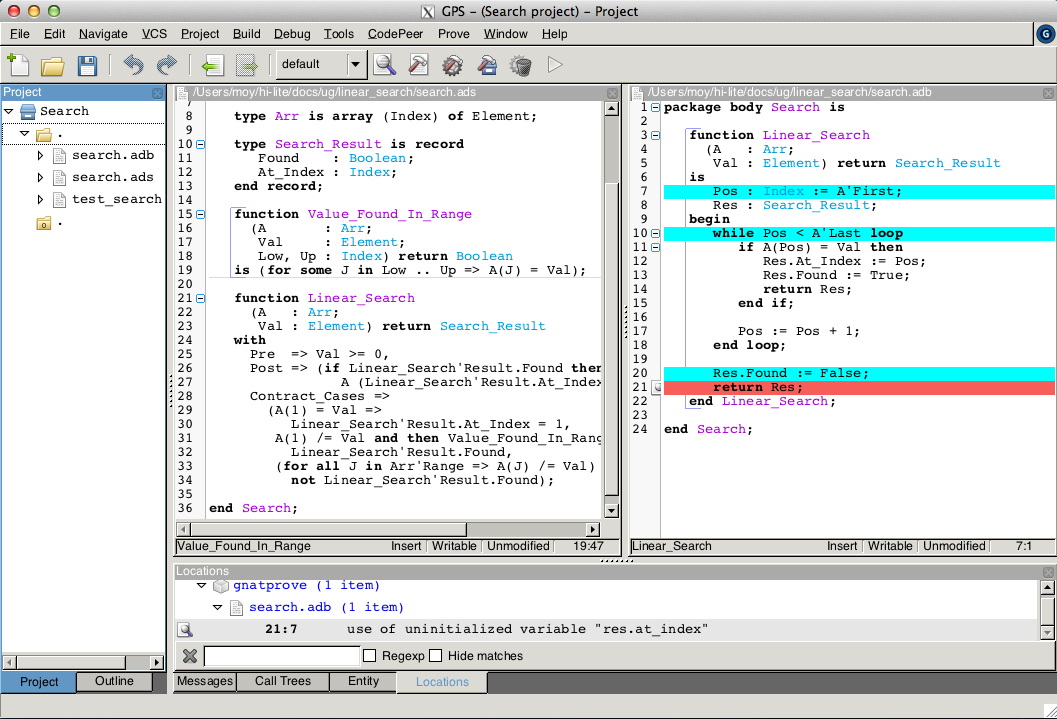
search.adb:21:07: use of uninitialized variable "res.at_index"

Inside the GPS editor, we can click on the path icon, either on the left of the message, or on line 21 in file search.adb, to show the path on which Res.At_Index is not initialized:

Note

If you use the SPARK-HiLite GPL 2013 release, the way to display a path in GPS is slightly different. Instead of clicking on an icon, you need to right-click on the error message in the Location View, and select Prove::Show Path in the contextual menu that is raised.

This shows that, when the value is not found, indeed the component At_Index of the value returned is not initialized. Although that’s allowed in Ada, SPARK 2014 requires that all inputs and outputs of subprograms are completely initialized (and the value returned by a function is such an output). Although we could give a dummy value to component At_Index when the search fails, we choose to turn the type Search_Result into a discriminant record, so that the component At_Index is only usable when the search succeeds:

type Search_Result (Found : Boolean := False) is record
   case Found is
      when True =>
         At_Index : Index;
      when False =>
         null;
   end case;
end record;

Then, in the implementation of Linear_Search, we change the value of the discriminant depending on the success of the search:

function Linear_Search
  (A   : Arr;
   Val : Element) return Search_Result
is
   Pos : Index := A'First;
   Res : Search_Result;
begin
   while Pos < A'Last loop
      if A(Pos) = Val then
         Res := (Found    => True,
                 At_Index => Pos);
         return Res;
      end if;

      Pos := Pos + 1;
   end loop;

   Res := (Found => False);
   return Res;
end Linear_Search;

GNATprove runs without errors in mode flow on this program, which shows there are no reads of uninitialized data.

We continue with the proof of contracts and absence of run-time errors, using the main mode prove of GNATprove, in the Prove::Prove File menu. It completes in a few seconds, with messages stating that 3 checks could not be proved:

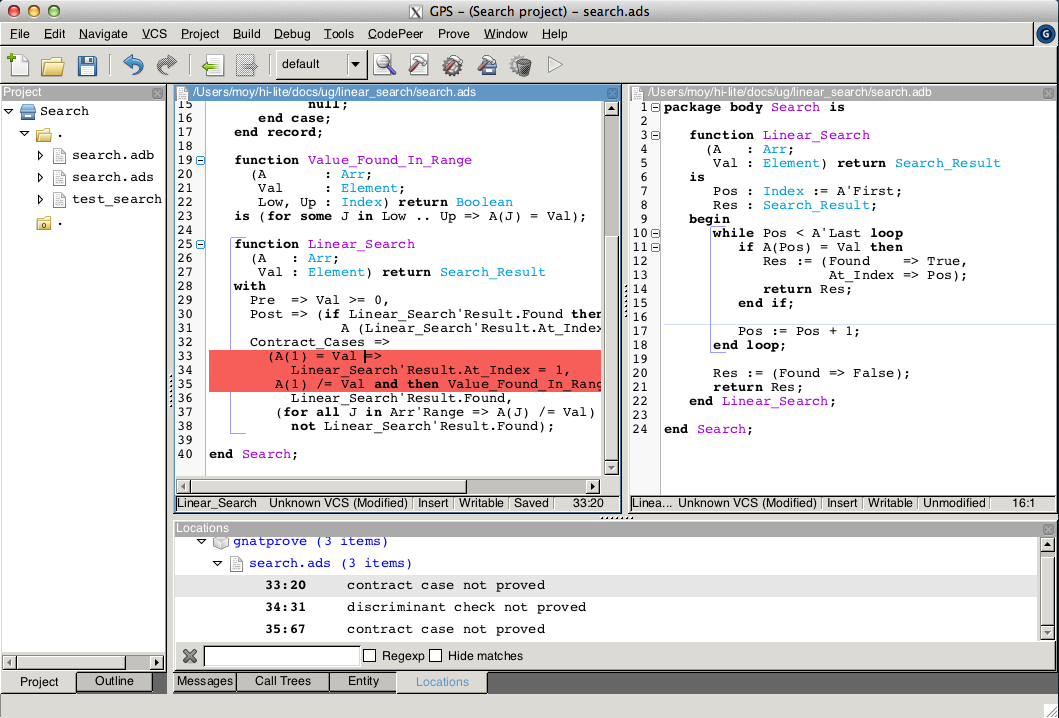
Note that there is no such message on the postcondition of Linear_Search, which means that it was proved. Likewise, there are no such messages on the body of Linear_Search, which means that no run-time errors can be raised when executing the function.

All 3 unproved checks are checked when exiting from Linear_Search. It is expected that not much can be proved at this point, given that the body of Linear_Search has a loop but no loop invariant, so the formulas generated for these checks assume the worst about locations modified in the loop. A loop invariant is a special pragma Loop_Invariant stating an assertion in a loop, which can be both executed at run-time like a regular pragma Assert, and used by GNATprove to summarize the effect of successive iterations of the loop. We need to add a loop invariant stating enough properties about the cumulated effect of loop iterations, so that the contract cases of Linear_Search become provable. Here, it should state that the value searched was not previously found:

pragma Loop_Invariant
  (not Value_Found_In_Range (A, Val, A'First, Pos));

As stated above, this invariant holds exactly between the two statements in the loop (after the if-statement, before the increment of the index). Thus, it should be inserted at this place. With this loop invariant, two checks previously not proved are now proved, and a check previously proved becomes unproved:

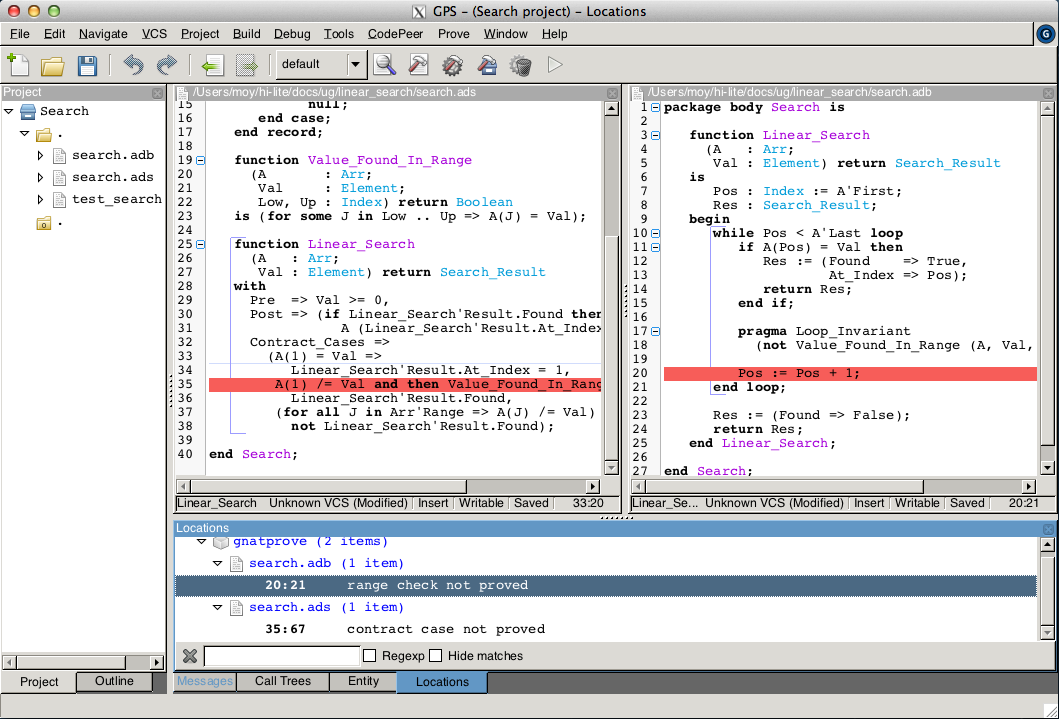
The new unproved check may seem odd, since all we did was adding information in the form of a loop invariant. The reason is that we also removed information at the same time. By adding a loop invariant, we require GNATprove to prove iterations around the (virtual) loop formed by the following steps:

1. Take any context satisfying the loop invariant, which summarizes all previous iterations of the loop.
2. Execute the end of a source loop iteration (just the increment here).
3. Test whether the loop exits, and continue with values which do not exit.
4. Execute the start of a source loop iteration (just the if-statement here).
5. Check that the loop invariant still holds.

Around this virtual loop, nothing guarantees that the index Pos is not the maximal index at step 2 (the increment), so the range check cannot be proved. It was previously proved because, in absence of a loop invariant, GNATprove proves iterations around the source loop, and then we get the information that, since the loop did not exit, its test Pos < A'Last is false, so the range check can be proved.

We solve this issue by setting the type of Pos to the base type of Index, which ranges past the last value of Index:

Pos : Index'Base := A'First;

And we add the range information for Pos in the loop invariant:

pragma Loop_Invariant
  (Pos in A'Range
     and then
   not Value_Found_In_Range (A, Val, A'First, Pos));

This allows to prove the range check on line 21, but the loop invariant preservation becomes unproved:

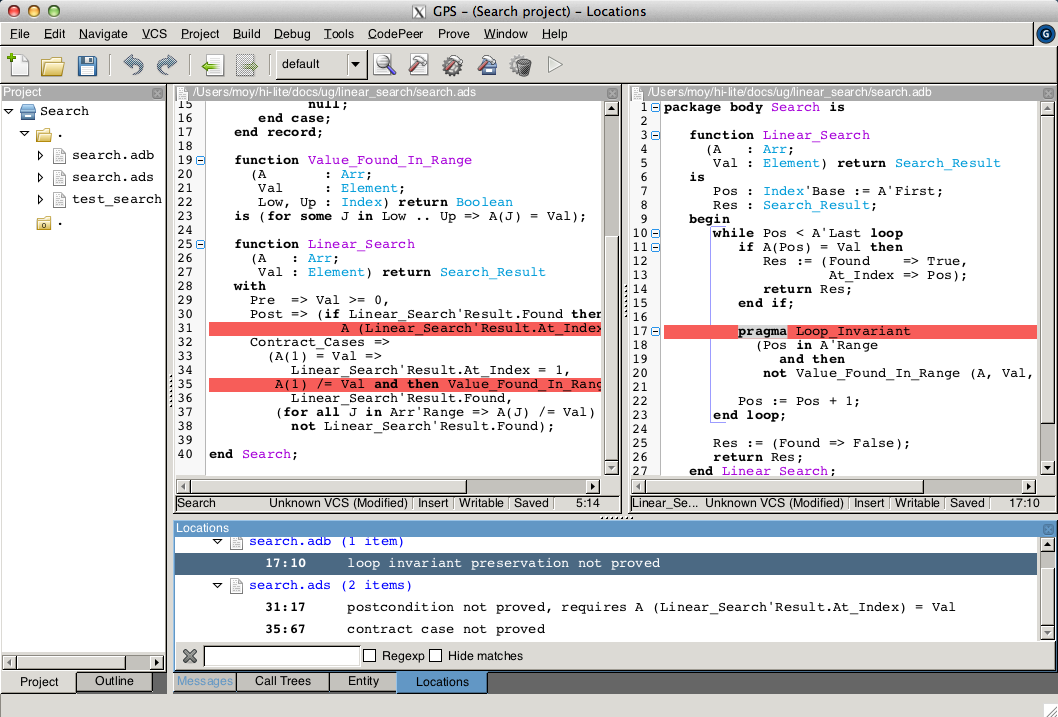
This is actually progress! Indeed, the loop invariant should be strong enough to:

1. prove the absence of run-time errors in the loop and after the loop
2. prove that it is preserved from iteration to iteration
3. prove the postcondition and contract cases of the subprogram

So we have just achieved goal 1 above! And the currently unproved preservation of the loop invariant is goal 2.

As we have modified the code and annotations, it is a good time to compile and run our test program, before doing any more formal verification work. This helps catching bugs early, and it’s easy to do! In particular, the loop invariant will be dynamically checked at each iteration through the loop. Here, testing does not show any problems:

$ gnatmake -gnata test_search.adb
$ test_search
> OK: Found existing value at first index
> OK: Did not find non-existing value

The next easy thing to do is to increase the timeout of the automatic prover. Its default of 1s is voluntarily low, to facilitate interaction with GNATprove during the development of annotations, but it is not sufficient to prove the more complex checks. Let’s increase it to 10s, and rerun GNATprove:

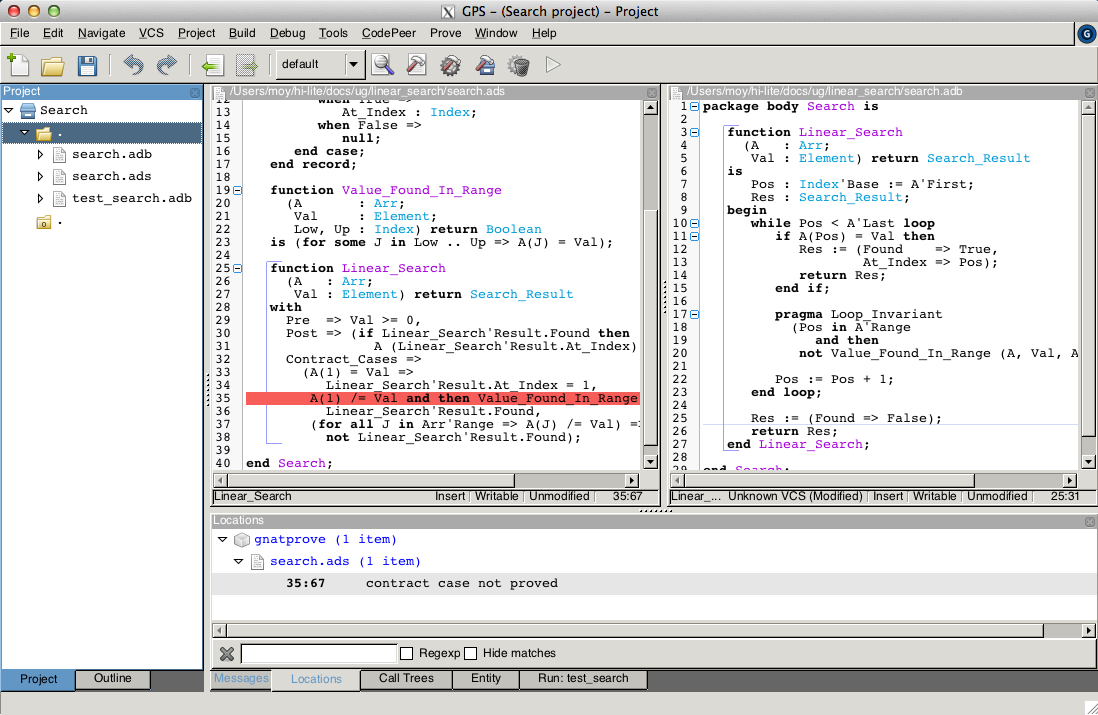
The loop invariant preservation was proved! One unproved check remains, in the contract cases of Linear_Search. We need to check that the loop invariant is strong enough to prove the unproved contract case (goal 3 above). To help with this assessment, we use the Prove Line contextual menu available on line 35:

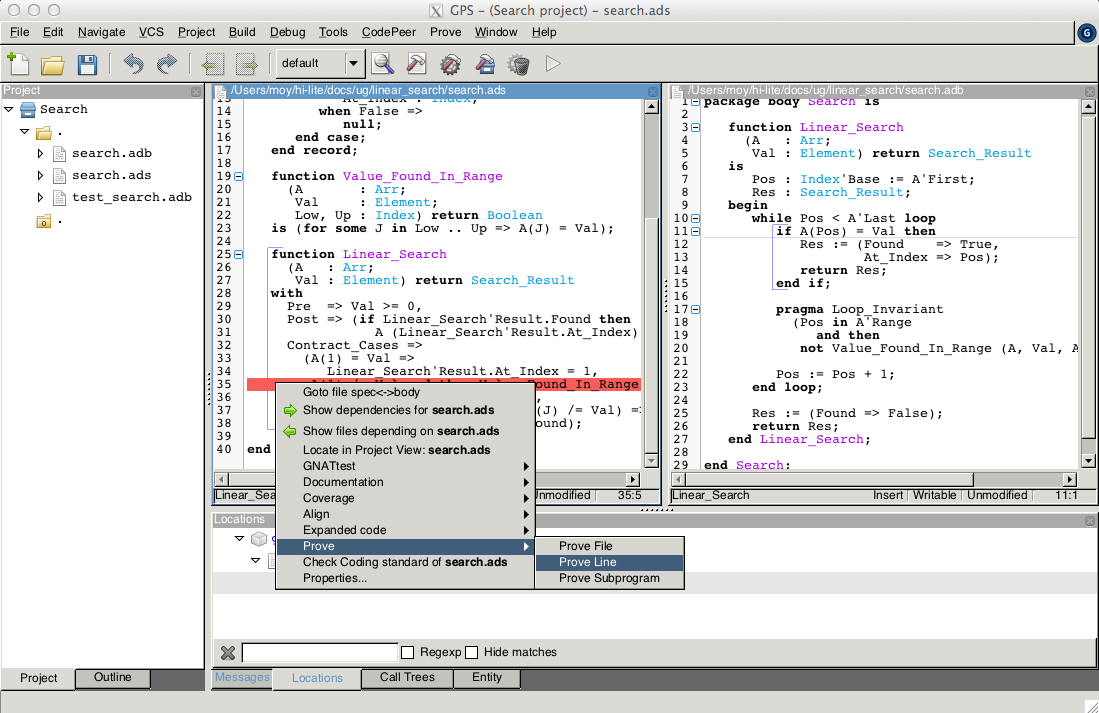
This runs GNATprove only on the checks that originate from line 35, in a special mode which considers separately individual execution path if needed. The check is still not proved, but GPS now displays an icon, either on the left of the message, or on line 35 in file search.ads, to show the path on which the contract case is not proved:

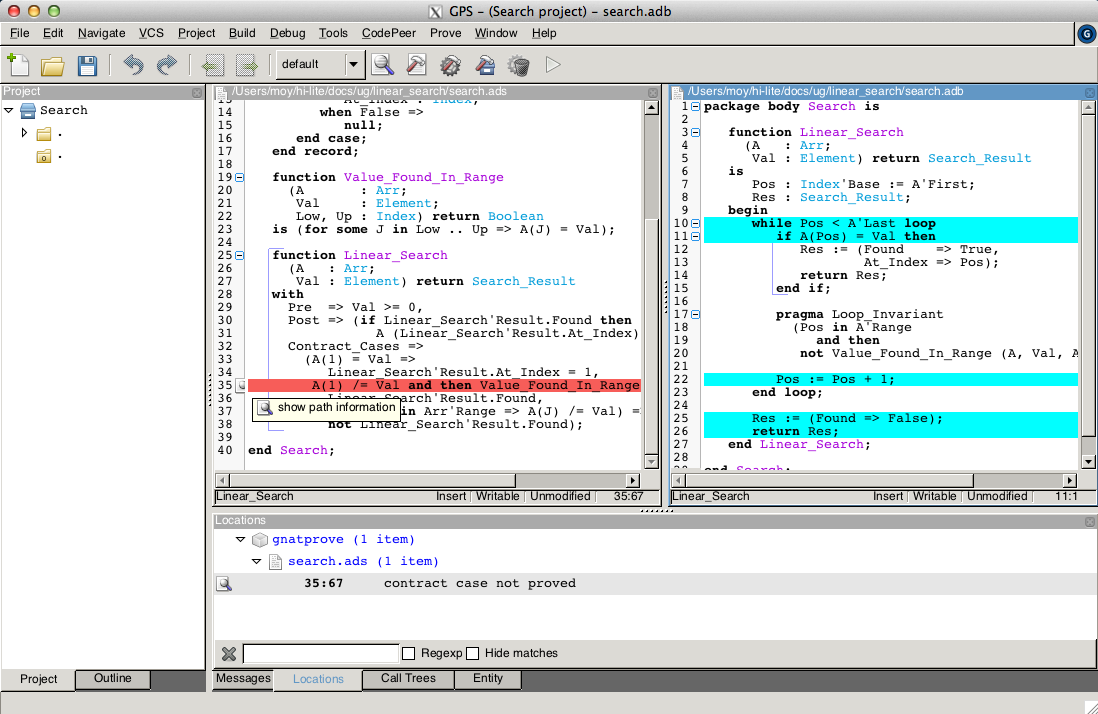
Note

If you use the SPARK-HiLite GPL 2013 release, the way to display a path in GPS is slightly different. Instead of clicking on an icon, you need to right-click on the error message in the Location View, and select Prove::Show Path in the contextual menu that is raised.

This corresponds to a case where the implementation of Loop_Search does not find the searched value, but the guard of the second contract case holds, meaning that the value is present in the range 2 to 10. Looking more closely at the path highlighted, we can see that the loop exits when Pos = A'Last, so the value 10 is never considered! We correct this bug by changing the loop test from a strict to a non-strict comparison operation:

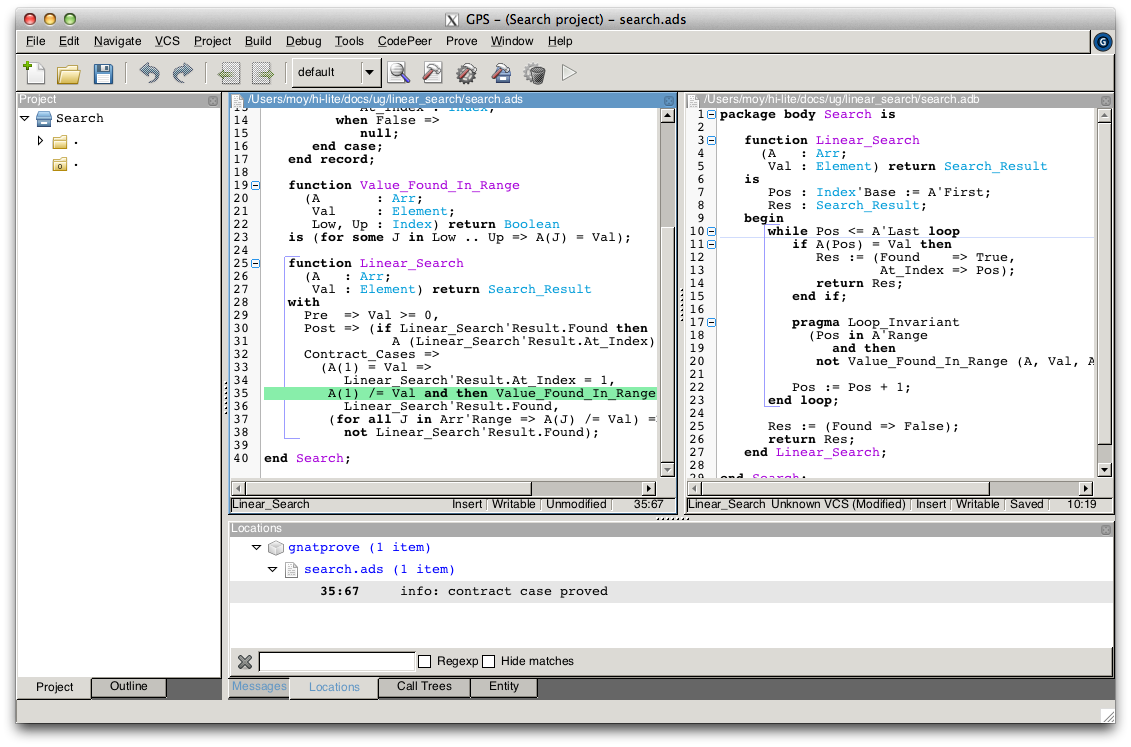
while Pos <= A'Last loop

On this modified code, we rerun GNATprove on line 35, checking the box Report Proved VCs to get information even when a check is proved. The reassuring green color (and the accompanying info message) show that the check was proved this time:

Like usual after code changes, we rerun the test program, which shows no errors. Rerunning GNATprove on the complete file shows no more unproved checks. The Search unit has been fully proved. To see all the checks that were proved, we can rerun the tool with box Report Proved VCs checked, which displays the results previously computed:

Note that one thing that was not proved is that Linear_Search terminates. As it contains a while-loop, it could loop forever. To prove that it is not the case, we add a loop variant, which specifies a quantity varying monotonically with each iteration. Since this quantity is bounded by its type, and we have proved absence of run-time errors in Linear_Search, proving this monotonicity property also shows that there cannot be an infinite number of iterations of the loop. The natural loop invariant for Linear_Search is the index Pos, which increases at each loop iteration:

pragma Loop_Variant (Increases => Pos);

With this last modification, the test program still runs without errors (it checks dynamically that the loop variant is respected), and the program is still fully proved. Here is the final version of Search, with the complete annotations:

pragma SPARK_Mode (On);

package Search is

   type Index is range 1 .. 10;
   type Element is new Integer;

   type Arr is array (Index) of Element;

   type Search_Result (Found : Boolean := False) is record
      case Found is
         when True =>
            At_Index : Index;
         when False =>
            null;
      end case;
   end record;

   function Value_Found_In_Range
     (A       : Arr;
      Val     : Element;
      Low, Up : Index) return Boolean
   is (for some J in Low .. Up => A(J) = Val);

   function Linear_Search
     (A   : Arr;
      Val : Element) return Search_Result
   with
     Pre  => Val >= 0,
     Post => (if Linear_Search'Result.Found then
                A (Linear_Search'Result.At_Index) = Val),
     Contract_Cases =>
       (A(1) = Val =>
          Linear_Search'Result.At_Index = 1,
        A(1) /= Val and then Value_Found_In_Range (A, Val, 2, 10) =>
          Linear_Search'Result.Found,
        (for all J in Arr'Range => A(J) /= Val) =>
          not Linear_Search'Result.Found);

end Search;

pragma SPARK_Mode (On);

package body Search is

   function Linear_Search
     (A   : Arr;
      Val : Element) return Search_Result
   is
      Pos : Index'Base := A'First;
      Res : Search_Result;
   begin
      while Pos <= A'Last loop
         if A(Pos) = Val then
            Res := (Found    => True,
                    At_Index => Pos);
            return Res;
         end if;

         pragma Loop_Invariant
           (Pos in A'Range
              and then
            not Value_Found_In_Range (A, Val, A'First, Pos));
         pragma Loop_Variant (Increases => Pos);

         Pos := Pos + 1;
      end loop;

      Res := (Found => False);
      return Res;
   end Linear_Search;

end Search;

This concludes our initial tour of the SPARK 2014 toolset!